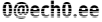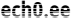Kuna ühiksubstitutsioon võrdub mistahes transpositsiooni ruuduga, siis
vaatleme substitutsioone, mis ei ole ühiksubstitutsioonid. Kuna kõik
permutatsioonid n elemendist on võimalik niiviisi järjestada, et
iga järgnev permutatsioon on eelnevast saadav transpositsiooni abil,
kusjuures esimeseks võib valida suvalise permutatsiooni, siis on
järelikult võimalik ka kõik substitutsioonid n elemendist
niiviisi ära järjestada, et alustame ühiksubstitutsioonist ning iga
järgneva substitutsiooni normaalkuju alumise rea permutatsioon on
saadud eelneva substitutsiooni normaalkuju alumise rea permutatsioonist
transpositsiooni abil. Mingi substitutsiooni korrutamine paremalt
transpositsiooniga, mille ülemises reas on mingitel kohtadel i
ja j, kusjuures i asub j-st eespool, ja alumisel
vastavalt samadel kohtadel j ja i (siis j asub
i-st eespool), on samaväärne i-nda ja j-nda
elemendi ümbervahetamisega selle substitutsiooni normaalkuju alumises
reas, see tähendab transpositsiooniga selle substitutsiooni normaalkuju
alumises reas asetsevas permutatsioonis. Järelikult on mistahes
substitutsioon siis ühiksubstitutsiooni ja teatava arvu
transpositsioonide korrutis. Kuna ühiksubstitutsiooni ärajätmine
sellest korrutisest korrutist ei muuda, siis iga substitutsioon
vähemalt kaheelemedilisel hulgal on esitatav transpositsioonide
korrutisena. m1n1mAALnE GRAAf 0n tR1AnGuLAts100n 
Olgu G minimaalne graaf ning olgu ta tasandile joonistatud nii, et tema
mingil tahul on rohkem kui kolm külge. Valime ühe sellise tahu piirilt
kaks tippu v ja w, mis ei ole teineteise naabertippudeks.
Ühendame nüüd tipud v ja w uue servaga ning surume
selle serva kokku üheks punktiks. Tulemuseks on uus (aga väiksema
tippude arvuga) tasandiline graaf G'. Et G oli minimaalne graaf,
siis on G' nelja värviga värvitav. On selge, et iga graafi
G' värvimismoodus indutseerib esialgse graafi värvimismooduse
(mille korral tipud v ja w on värvitud ühe ja sama
värviga). Sellega on näidatud, et minimaalse graafi ühegi tahu
piiril ei saa olla rohkem kui kolm serva. Järelikult on minimaalne graaf
triangulatsioon. 1GA sAmAm22RAtAvAtE juhusL1kE suuRustE huLk s1sALduB m1nG1s (m1n1mAALsEs) juhusL1kE suuRustE Ruum1s 
Vaatleme katset, mis määrab kõik antud samamääratavad
juhuslikud suurused. Kõigi selle katse võimalike tulemuste
funktsioonide hulk (st. kõigi juhuse funktsioonide hulk) on viie
põhiomadusega ja sisaldab seejuures etteantud juhuslike suuruste hulga.
Nii oleme saanud juhuslike suuruste ruumi, kus sisaldub etteantud juhuslike
suuruste hulk, kuid üldiselt võib leiduda teisigi (vaesemaid)
juhuslike suuruste ruume, mis sisaldavad sama juhuslike suuruste hulga. On aga
õige lihtne näha, et kõigi nende ruumide ühine osa ei ole
tühi ja on seejuures jälle juhuslike suuruste ruum. Viimane on
ilmselt minimaalne juhuslike suuruste ruum, kus sisaldub etteantud juhuslike
suuruste hulk. Teoreem on tõestatud. k0Lm ALGEBRAL1st L61ku 
Järelikult iga poolrühm (muuseas ka iga rühm) on isomorfne selle poolrühma elementide hulga mingi teisenduste poolrühmaga. Kuna rühmaga isomorfne poolrühm on ise rühm, teisenduste seas aga omavad pöördelementi ainult üksühesed teisendused, siis järeldub siit otsekohe, et iga rühm on isomorfne selle rühma elemetide hulga mingi üksüheste teisenduste rühmaga. Lõplike rühmade jaoks seega iga lõplik rühm on isomorfne mingi substitutsioonide rühmaga. Tetraeedri liikumiste rühm koosneb kaheteistkümnest elemendist: ühikelemendist, kaheksast liikumisest, mis jätavad paigale ühe tippudest ja teostavad pöörde seda tippu ning tema vastastahu keskpunkti läbiva sümmeetriatelje ümber, ning kolmest pöördest vastasservade keskpunkte ühendava kolme sümmeetriatelje ümber. Lihtne on veenduda, et kõikidele nendele liikumistele vastavad tippude paarissubstitutsioonid. Seega on tetraeedri liikumiste rühm isomorfne vahelduva rühmaga A4. Üldse koosnevad korrapäraste hulktahukate liikumiste rühmad ainult pööretest, mistõttu neid nimetatakse pöörete rühmadeks.
Esimeseks teadusalaks, milles rühmateooriat rakendati sügavate probleemide
lahendamiseks, osutus omal ajal kristallograafia. Nimelt klassifitseeris tuntud vene
matemaatik J. S. Fjodorov 1890. a. kõik korrapärased ruumvõred, kasutades
seejuures selliste võrede sümmeetriarühmi. Selgus, et niisuguseid
rühmi - neid nimetatakse kristallograafilisteks rühmadeks ehk Fjodorovi
rühmadeks - on 230, kusjuures 65 rühma ei sisalda peegeldusi ja 165 sisaldavad
neid. Mõistagi, et kristallograafid ei suutnud enne rühmateooria
kasutuselevõtmist ise anda sellist ammendavat klassifikatsiooni ning pidid piirduma
palju jämedama liigitusega. BEEtAtR0n 
Pööriselektrivälja kasutatakse elektronide induktsioonikiirendis, mida
nimetatakse beetatroniks. Beetatron koosneb elektromagnetist, mille erilise kujuga
pooluskingade vahele paigutatakse vaakumkamber. Elektromagneti mähist toidetakse
vahelduvvooluga, mille sagedus on ~100 Hz. Seejuures tekkival vahelduvmagnetväljal on
täita kaks funktsiooni: ta indutseerib elektrone kiirendava
pööriselektrivälja ja hoiab osakesi kambri teljega ühtival orbiidil.
c0mpAct d1sc 
In storing and handling the Compact Disc, you should apply tha same care as with
conventional records. No further cleaning will be necessary if the Compact Disc
is always held by the edges and is replaced in its case directly after playing.
Should the Compact Disc become soiled by fingerprints, dust or dirt, it can be
wiped (always in a straight line, from center to edge) with a clean and lint-free,
soft dry cloth. No solvent or abrasive cleaner should ever be used on the disc.
If you follow these suggestions, the Compact Disc will provide a lifetime of
pure listening enjoyment. 1nvERssEtEst p00LRyhmAdEst 
Alates m2rtsist on mul peas olnud yks idee vaadata inverssete poolryhmade
teatud alampoolryhmi. Ja olengi defineerinud hariliku regulaarsuse asemel
2-regulaarsuse (mida annab yldistada n-regulaarsusesks) ja 2-inverssuse
(annab yldistada n-inverssuseks). Regulaarne
poolryhm on inversne parajasti siis, kui tema idempotendid kommuteeruvad.
Ma n2itasin, et 2-inverssusest j2reldub inverssus ja 2-regulaarsusest
regulaarsus (viimane on absoluutselt ilmne, kui teada definitsioone). Mul
6nnestus n2idata, et 2-inversse poolryhma idempotendid kommuteeruvad ka,
suure vaeva ja raskusega, kuigi oleks saanud lihtsamalt, nagu hiljem
m2rkasin, lihtsalt yhe j2reldusena. Aga idempotentide kommuteeruvusest ma
ei suutnud j2reldada, et 2-regulaarne poolryhm on 2-inversne. See oli
kohutav uudis minu jaoks. Nyyd ma pean m6tlema v2lja mingi uue tarviliku
ja piisava tingimuse, et 2-regulaarne poolryhm oleks 2-inversne. Yks idee
ka on, aga seda teostama hakates pole mul enam kusagilt eeskuju v6tta,
t2iesti ise ja yksinda pean seda tegema, kui tahan. k0Lm t0p0L00G1L1st L61ku 
Tasandil on kinnise hulga näiteks paralleelsirgete vaheline riba koos nende äärsirgetega. Tõepoolest, selle riba täiendiks on kahe äärsirgeta pooltasandi ühend, kumbki neist on aga lahtine, mistõttu ka see ühend on lahtine. Kinnine on järelikult ka rööpkülik (koos tippude ja külgedega), sest ta on kahe kõnesoleva riba ühisosa.
Möbiuse lehe iseärasus on selles, et temal liikudes piki keskjoont tuleb
kujund tagasi mitte algasendis, vaid peegeldatud asendis ja alles pärast teistkordset
läbimist saame algasendi uuesti kätte. Seda asjaolu väljendatakse
öeldes, et Möbiuse leht pole orienteeritav. Näiteks positiivne
pöördesuund (vastu kellaosuti liikumist) kaotab temal mõtte, sest
pärast liikumist piki keskjoont tuleb kell tagasi peegeldatult.
Antud punktis algavate ja lõppevate ringliinide homotoopsusklassid moodustavad
rühma, kui nende klasside hulgas defineerida korrutamine selliselt, et kahe
klassi korrutiseks on neist klassidest võetud ringliinide liitliini klass
(mis ei sõltu nende ringliinide valikust nendes klassides). Ühikuks on
püsiliini klass, antud klassi pöördelemendiks - selle klassi liini
pöördliini klass (mis samuti ei sõltu liini valikust antud klassis).
k0Lm k0mB1nAt00R1kA L61ku 
Iga fikseeritud substitutsioon g jaotab hulga S tsüklite kui ühisosata alamhulkade summaks (ühendiks), kusjuures liidetavate komplekt on üheselt määratud. Kui veel igas tsüklis elemendid teatud viisil järjestada, siis on substitutsioon täielikult kirjeldatav oma tsüklite kaudu. Esituse ühesuse saavutamiseks lepitakse tavaliselt kokku alustada iga tsükli kirjutamist tema vähima elemendiga (hulgas S määratud "loomuliku" järjestuse mõttes), esitada tsüklid nende pikkuste mittekahanevas järjekorras ning ühepikkused tsüklid näiteks nende esimeste elementide kasvavas järjekorras.
Nagu algebrast teada, saab suvalise substitutsiooni esitada transpositsioonide
korrutisena. Niisuguses esituses pole küll üheselt määratud ei tegurid
ise ega nende täpne järjekord, kuid üheselt määratuks osutub
tegurite arvu paarsus. Paarisarvu transpositsioonide korrutisena avalduvaid substitutsioone
nimetatakse paarissubstitutsioonideks, ülejäänuid aga paarituteks.
Ilmselt on nii paarissubstitutsioonide korrutis kui ka samuti ühiksubstitutsioon
paaris. Seega kõikide paarissubstitutsioonide hulk moodustab sümmeetrilises
rühmas alamrühma (mida algebras nimetatakse enamasti
märgivahetusrühmaks).
Igal kumeral hulktahukal leidub alati kaks tahku, mida piirab ühesugune arv
servi. Tõepoolest, olgu hulktahuka tahku piiravate servade maksimaalarvuks
n. Lahterdame kõik tahud neid piiravate servade arvu järgi pesadesse
märgenditega 3, 4, ..., n. Et tahk, mida piirab n serva, külgneb
n erineva tahuga, siis tahkude üldarv pole väiksem kui n+1.
Dirichlet' printsiibist tulenevalt peab ühte pesadest 3, 4, ..., n nüüd
sattuma vähemalt kaks erinevat tahku, millel seega ongi ühepalju piiravaid servi.
k0nt11numhyp0tEEs 
1878. aastal püstitas Georg Cantor hüpoteesi, mille kohaselt ei leidu hulka,
mille võimsus oleks suurem kui loenduva hulga võimsus ning väiksem kui
kontiinumi võimsus (nn. kontiinumhüpotees). 1940. aastal tõestas
Kurt Gödel, et kui teatud mittevasturääkivale hulgateooria aksioomide
süsteemile lisada valikuaksioom ja kontiinumhüpotees, siis saadakse
mittevasturääkiv aksioomide süsteem. 1963. a. näitas Paul Cohen, et
samast aksioomide süsteemist saadakse mittevasturääkiv aksioomide
süsteem ka siis, kui sellele lisada valikuaksioomi ja kontiinumhüpoteesi eitused.
Seega - veidi lihtsustatult öeldes - on mõeldav hulgateooria, mille aksioomide
hulgas on kontiinumhüpotees, kui ka hulgateooria, mille aksioomide hulgas on
kontiinumhüpoteesi eitus. vAL1kuAks100m1st 
Probleem, kuivõrd on õigustatud valiku aksioomi lülitamine
hulgateooria aksiomaatikasse, on erutanud paljusid matemaaikuid. Esimesel pilgul
võib näida, et mingit probleemi ei ole. Seisneb ju valikufunktsiooni
määramine valiku teostamises iga indeksi i jaoks: igast hulgast
Ai tuleb valida mingi element f(i). Kuna Ai
on mittetühi, siis iga i korral eraldi muidugi saab sellise valiku teostada.
Probleem on aga selles, et kui hulk I on lõpmatu ja meil puudub igasugune
informatsioon hulkade Ai kohta, siis ei ole võimalik ühtegi
konkreetset valikufunktsiooni konstrueerida lõpliku arvu sammude jooksul. Kui me
valiku aksioomi kehtivaks tunnistame, siis osutub võimalikuks selliste objektide
olemasolu tõestamine, mida me ei ole suutelised reaalselt konstrueerima. Just see
ongi põhjus, miks rida matemaatikuid ei pea valiku aksioomi kasutamist
õigustatuks. Meie loeme oma käsitluses valiku aksioomi kehtivaks, asudes
sellega ühel positsioonil rõhuva enamiku matemaatikutega. Seda positsiooni
võiks kaitsta järgmise mõttega: mõnikord on kasulik teada
mõne asja olemasolust vaatamata sellele, et me seda esialgu konstrueerida ei oska.
k0Lm kAtEG00R1L1st v21dEt 
Kui kategoorias on olemas igale morfismipaarile vastav konservatiivne ruut ja lõppobjekt, siis on kategooria igal objektipaaril olemas korrutis. Kui kategooria igal kahel objektil on olemas korrutis ja igal kahel alamobjektil lõige, siis on selles kategoorias olemas iga morfismipaari võrdsustaja.
Kui kategoorias on olemas objektide lõplikud korrutised, igal objektipaaril on
olemas võrdsustaja ja igal lõplikul alamobjektide süsteemil on olemas
lõige, siis on antud kategoorias olemas kõikvõimalikud lõplikud
piirid.
kAks kAtEG00R1L1st L61ku 
See, et funktorid säilitavad isomorfismid, on tõenäoliselt kõige olulisem põhjus, miks funktoreid uurima asuti. On ju kõikides matemaatilistes teooriates üheks oluliseks küsimuseks selle teooria objektide isomorfsuse küsimus. Kui see mingis situatsioonis on keeruline, aga on kirjeldatav kategooriate keeles ning meil on sellest kategooriast olemas funktor mõnda teise kategooriasse, kus objektide isomorfsuse küsimus on lihtsamini käsitletav, siis me oleme ühe kategooria keerulise probleemi taandanud teise kategooria lihtsamale probleemile. Topoloogia, eriti algebralise topoloogia, küsimuste lahendamisel kasutatakse seetõttu väga tihti funktoreid, mis viivad rühmade (sagedasti ka Abeli rühmade) kategooriasse, ning taandatakse sageli keeruliselt käsitletavad homöomorfsuse küsimused rühmade isomorfsuse küsimustele.
Kategooria objektide alamklassi koos kõigi nende objektide vaheliste morfismidega
nimetatakse täielikuks alamkategooriaks. Kategooria
K täielikku alamkategooriat
L, mis iga kategooria K
objekti korral sisaldab täpselt ühe temaga isomorfse objekti, nimetatakse
kategooria K skeletiks. Kategooriat
nimetatakse kõhnaks, kui ta langeb kokku oma skeletiga. On
võimalik tõestada, et kaks kategooriat on ekvivalentsed siis ja ainult siis,
kui kui nende skeletid on isomorfsed.
k0Lm tE0REEt1L1s-mEhAAn1kAL1st L61ku 
Arutleme nüüd järgmiselt: kui seose reaktsioonjõud on just niisugune jõud, mis sunnib punkti liikuma nii, nagu seda teeb seos, siis võib alati kujutleda seose hoopis eemaldatuna ning tema mõju punkti liikumisele asendatuna seose reaktsioonjõuga. Me võime kujutleda, et matemaatiline pendel ei liigu ringjoont mööda mitte sellepärast, et ta on kinnitatud niidi otsa, vaid sellepärast, et teda sunnib nii liikuma jõud - niidi tõmme; mitte et laual asetsev keha on tasakaalus sellepärast, et laud ei luba tal oma kaalu mõjul vabalt langeda, vaid sellepärast, et raskusjõuga võrdvastupidine jõud (laua reaktsioon) tasakaalustab viimase jne. Nii võime alati, kui see on vajalik, üle minna mittevabalt masspunktide süsteemilt vabale süsteemile, kui vaid lisame selle süsteemi punktidele mõjuvaile jõududele seoste reaktsioonid. Seda tehes ütleme, et kasutame seostest vabastatavuse printsiipi. Maa pinnal või selle läheduses liikuv keha kaldub Maa pöörlemise tõttu põhjapoolkeral liikumissuunast paremale, lõunapoolusel aga vasakule. Selle reegli kinnituseks võib tuua mitmeid fakte. Reeglis ennustatud kõrvalekalle ilmneb näiteks mürskude ja kaugrakettide lennu juures. Läbiviidud vaatlused näitavad, et Coriolise inertsjõu tõttu on põhjapoolkeral voolavate jõgede paremad kaldad enam uhutud kui vasemad (Baeri seadus). On täheldatud, et rongide ühesuunalise liikumise puhul kulub põhjapoolkeral parempoolne rööbas kiiremini. Maakera pöörlemise mõjuga on seletatav ka passaattuulte kõrvalekaldumine põhja-lõuna suunast.
Planeet liigub liikuva Päikese suhtes nii, nagu ta liiguks liikumatu Päikese
suhtes, kui selle mass oleks suurendatud planeedi massi võrra. Muide, viga,
mille teeme Päikest paigalseisvaks lugedes, on väike, sest võrreldes
planeediga on Päikese mass väga suur (suurima planeedi Jupiteri mass moodustab
kõigest 0,1% Päikese massist). Kuna planeedi ja Päikese kaugused
masskeskmest on võrdelised Maa ja Päikese vahelise kaugusega, siis võib
järeldada, et ka planeedi ja Päikese trajektoorid masskeskme suhtes on ellipsid.
Planeedi trajektooriks on ellips, mis peaaegu ei erine sellest, mille ta kujundaks juhul,
kui Päike oleks liikumatu; Päikese poolt kujundatav ellips on planeedi omaga
võrreldes väga väike. (Muide, näiteks süsteemi Maa - Päike
masskese asetseb Päikese sees, vähem kui 500 km Päikese masskeskmest Maa
suunas).
k0Lm EkstREEmsEt 0BjEkt1 
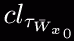 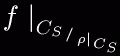 tuli ette aines "Algebra struktuurid". Ja lõpuks, et 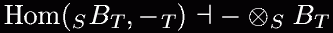 , ,[Enda tähelepanekutest Tartu Ülikoolis matemaatika-informaatikateaduskonnas 1998-2004 puhast matemaatikat õppides.] k0Lm mAtEmAAt1L1sE L00G1kA L61ku 
Tuletamine igas formaalses teoorias kujutab endast mängu sümbolitega. Selle mängu reegleid nimetatakse teooria süntaksiks. Peale selle võib teooria valemitele olla omistatud mingisugune sisu, st. võib olla defineeritud, mida iga valem tähendab. Valemite tähendust nimetatakse vastava keele semantikaks. Näiteks, esimest järku keele korral defineerib iga interpretatisoon ühe semantika selle keele valemitele. Semantikat võib defineerida ka mingi interpretatsioonide klassi kaudu, seades igale valemile vastavusse väite, et see valem on tõene kõigis antud klassi kuuluvates interpretatsioonides (näiteks kõigil rühmadel või kõigil lõpmatutel mudelitel). Lausearvutuse valemitele võime seada vastavusse väite, et see valem on samaselt tõene. Paljudel juhtudel on alguses olemas teooria sisuline pool, st. uuritavad objektid, mille kohta mingi hulk fakte on juba teada. Teooria edasiarendamiseks või korrastamiseks valitakse valemite keel, mis võimaldab tähistada valdkonnas vaadeldavaid põhilisi konstante ja funktsioone ning väljendada teoorias kasutatavaid põhilisi predikaate. Selle keele semantika on juba algusest peale olemas. Aksioomid ja reeglid proovitakse valida nii, et formaalne aksiomaatiline teooria tuleks korrektne ja täielik, st. tuletatavateks valemiteks osutuksid parajasti need valemid, mis on semantikas tõesed. Matemaatilise loogika uurimused on näidanud, et paljudel tähtsatel juhtudel ei ole see võimalik (näiteks naturaalarvude aritmeetika korral). On selge, et mittekorrektne formalisatsioon, kus saaks tõestada ka mõnesid vääri valemeid, ei ole üldse vastuvõetav. Seega jääb üle rahulduda paratamatusega, et mõned tõesed valemid ei ole formaalses teoorias tuletatavad ja püüda jätta mittetuletatavad tõed teooria "ääremaadele".
Lahenduvuse probleem vajab iga esimest järku teooria korral eraldi uurimist.
On teada sadu teoreeme konkreetsete esimest järku teooriate lahenduvuse või
mittelahenduvuse kohta. Näiteks rühmateooria ei ole lahenduv, aga Abeli rühmade
teooria on seda. Võreteooria ja distributiivsete võrede teooria pole lahenduvad,
aga Boole'i algebrate teooria on lahenduv jne.
1GAs Es1mEst j2Rku tE00R1As 0n 1GA tuLEtAtAv sEkvEnts t6ene 1GAs 1ntERpREtAts100n1s, m1LLEs tE00R1A k61k 0mAAks100m1d 0n t6EsEd 
Tõepoolest. Induktsiooni baas peab ilmselt paika: iga aksioom on igas sellises
interpretatsioonis tõene. Sammu tõestuse saab predikaatarvutusest samuti
üle võtta. Tegelikult näitasime ka seal, et kui reegli ülemine
sekvents (ülemised sekventsid) on vaadeldavas interpretatsioonis antud vabade muutujate
väärtuste korral tõene (tõesed), siis on seda ka alumine sekvents.
Seega tuletuspuud mööda alla liikudes säilib tõesus igas fikseeritud
mudelis, järelikult ka kogu meid huvitavas mudelite klassis.
k0Lm 0pt1m1sEER1vAt L61ku 
Lihtne on veenduda, et kui sadulpunktiga mängu korral üks mängijaist kasutab oma ohutuimat
strateegiat, siis teine mängija ei saa oma ohutuimast strateegiast loobumisest kunagi kasu
(küll aga võib kahju saada). See tähendab, et mängija võib juba enne mängu algust vastasele
teatada oma kavatsuse kasutada ohutuimat strateegiat: seda informatsiooni ei saa vastane
enda võidu suurendamiseks kuidagi ära kasutada. Piiramata horisondi juhule minnakse praktikas üle enamasti siis, kui perioodi pikkus on suhteliselt lühike (näiteks päev), planeerida tuleb aga väga paljude perioodide jaoks (näiteks mitmeks aastaks). Tüüpiliseks piiramata horisondiga praktiliste ülesannete klassiks on näiteks partii suuruse määramine toomises ja üldse paljude hulgitootmisega seotud probleemid.
Seni vaadeldud kahes teenindussüsteemis me eeldasime, et nii tellimuste saabumise kiirus
kui ka teenindamise kiirus on konstandid, ei sõltu süsteemi seisundist. Ilmselt moodustab
see lihtsa erijuhu üldisemast süsteemist, kus need kiirused osutuvad süsteemi seisundi
funktsioonideks. nEL1 n21dEt kAAsfunkt0R1tEst 
Funktor F seab rühmale vastavusse tema faktorrühma kommutandi järgi (see on Abeli rühm), funktor G "unustab" ära, et rühm on just Abeli rühm. Funktor F seab kommutatiivsele nulliteguriteta ringile vastavusse tema jagatiste korpuse, funktor G "unustab" ära, et korpuse nullist erinevatel elementidel peab olemas olema pöördelement. Funktor F seab moodulile üle kommutatiivse ringi vastavusse tema tensorkorrutise mingi fikseeritud mooduliga üle selle ringi, funktor G seab moodulile vastavusse mooduli, mis koosneb kõigist homomorfismidest sellest fikseeritud moodulist vaadeldavasse moodulisse.
Funktor F seab täielikult regulaarsele Hausdorffi ruumile vastavusse
tema Stone-Cechi kompaktse laiendi, funktor G "unustab" ära kompaktsuse.
P01ncARE k0GEmus 
Neliteist päeva olin maadelnud tõestusega, et ei leidu analoogseid funktsioone minu poolt Fuchsi funktsioonideks nimetatutega; tammusin täielikus pimeduses. Iga päev asusin oma töölaua taha ja katsetasin üks või kaks tundi edutult suurt hulka kombinatsioone. Ühel õhtul jõin vastupidi oma harjumustele tassi musta kohvi; ma ei saanud magama minna; ideed hõljusid mu ümber pilvedena; tundsin nende kuhjumist, kuni lõpuks üks paar ühines nii-öelda kindlaks blokiks. Koidikuks olin leidnud ühe klassi Fuchsi funktsioone, mis on tuletatud hüpergeomeetrilistest ridadest. Mul tarvitses tulemus kirja panna, milleks kulutasin mitu tundi. Seepeale tahtsin kujutada neid funktsioone kahe rea kordajatena; see eesmärk oli mulle hästi teada ja selge, kusjuures ajendiks oli analoogia elliptiliste funktsioonidega. Küsisin eneselt, millised omadused peaksid neil ridadel olema, kui sellised olemas on; moodustasin need raskusteta ja nimetasin nad teetafuchsilikeks. Seejärel lahkusin Caenist, kus ma tollal elasin, et võtta osa Mäeakadeemia poolt korraldatavast geoloogilisest ekskursioonist. Rännates olin sunnitud oma matemaatilised tööd unustama. Coutances'i saabunud, asusime ümber bussi. Sel silmapilgul, kui asetasin jala astmelauale, tuli mulle, nähtavasti ilma eelneva järelemõtlemiseta, idee, et teisendused, mida olin kasutanud Fuchsi funktsioonide defineerimisel, olid identsed mitteeukleidilise geomeetria omadega. Ma ei kontrollinud seda; mul poleks selleks aegagi olnud, sest bussis jätkasin katkenud vestlust, ometi tundsin vahetut ja täielikku kindlust. Naasnud Caeni, veendusin täielikus segamatuses oma idee õigsuses, et rahustada oma südametunnistust. Seejärel asusin suurema eduta uurima teatud aritmeetikaküsimusi, teadvustamata endale, et sel asjal oleks vähematki seost minu varasemate probleemidega. Siis sõitsin mõneks päevaks mere äärde ja mul olid teised asjad peas. Ühel päeval, kui läksin karidele jalutama, tuli mulle sama iseloomuliku ootamatuse ja vahetu kindlusega mõte, et kolmendruutvõrrandite teisendused on identsed mitteeukleidilise geomeetria omadega. Jõudnud tagasi Caeni, mõtlesin asja üle järele ja tegin vastavad järeldused; ruutvõrrandi näitest selgus mulle, et on olemas ka teisi Fuchsi rühmi, ja ma nägin, et saan neile rakendada teetafuchsilike funktsioonide teooriat. Selle kohaselt oli hüpergeomeetrilistest ridadest tuletatud funktsioonide kõrval veel teisi, mida ma varem ei tundnud. Loomulikult võtsin eesmärgiks leida kõik seda laadi funktsioonid. Alustasin kindluse süstemaatilist vallutamist ja allutasin ühe kantsi teise järel, otsustav kants osutas aga ikka veel vastupanu. Kõik minu ponnistused läksid tühja. See oli puhtteadlik töö.
Asjaolude selles staadiumis sõitsin Mont-Valerien'i, kus
pidin täitma oma sõjaväekohustust. Olin seetõttu haaratud
hoopis teistest probleemidest. Ühel päeval üle puiestee
minnes koitis mulle äkki, kuidas tekkinud raskusi ületada.
Ma ei püüdnudki sel silmapilgul oma mõtet arendada, vaid
võtsin probleemi käsile alles pärast teenistusaja lõppu.
Mul olid olemas kõik elemendid. Nad tuli ainult ühendada
ja korraldada. Nii panin töö kirja lõplikul kujul ja
raskusteta.
kyBERnEEt1kA ALGus 
Samal ajal aga oli ilmne, et arvutite ehitamisel on sõjaks ettevalmistumise mõttes palju suurem tähtsus kui doktor Bushi esialgse arvamuse järgi oleks võinud näida, ja see töö edenes eri keskustes sellises suunas, mis kuigi palju ei erinenud tollest, mille oli kätte näidanud minu varasem ettekanne. Harvard, Aberdeeni Katsepolügon ja Pennsylvania Ülikool juba ehitasid arvuteid ning peagi olid sellel alal tööle asumas ka Princetoni Kõrgemate Õpingute Instituut ja Massachusettsi Tehnoloogia Instituut. Selle töö käigus esines järkjärguline üleminek mehaaniliselt koostiselt elektrilisele koostisele, kümnendsüsteemilt kahendsüsteemile, mehaanilistelt releedelt elektrilistele releedele, inimese poolt suunatavalt tegutsemiselt automaatselt suunatavale tegutsemisele ja, lühidalt öeldes, vastas iga uus arvuti rohkem kui eelmine neile märkustele, mis ma doktor Bushile olin saatnud. Pidevalt lahkus ja saabus neid, kes nende alade vastu huvi tundsid. Meil oli soodne võimalus teha endi mõtted teatavaks oma ametivendadele, eriti doktor Aikenile Harvardist, doktor von Neumannile Kõrgemate Õpingute Instituudist ja doktor Goldstine'ile masinate ENIAC ja EDVAC juurest Pennsylvania Ülikoolis. Kõikjal sattusime me kuulajatele, kes elasid meile kaasa, ja inseneride sõnastikku hakkas peagi segunema neurofüsioloogide ning psühholoogide oskussõnu.
Asjaolude sellist arengut arvestades pidasime doktor von Neumann ja mina
soovitavaks korraldada ühine nõupidamine kõigi nendega, kes tundsid huvi
selle vastu, mida me nüüd nimetame küberneetikaks, ja see nõupidamine
leidis aset Princetonis 1943.-1944. aasta talve lõpupoole. Insenerid,
füsioloogid ja matemaatikud, kõik olid esindatud. Doktor Rosenbluethi
viibimine meie hulgas osutus võimatuks, sest ta oli äsja võtnud vastu
kutse tegutseda füsioloogialaboratooriumide juhatajana Rahvuslikus
Kardioloogia Instituudis Mehhikos, kuid füsiolooge esindasid doktor
McCulloch ja doktor Lorente de Nó Rockefelleri Instituudist. Doktor
Aikenil polnud võimalik kohal viibida; ent doktor Goldstine oli üheks
mitmete arvutite loojate rühmast, kes nõupidamisest osa võttis, doktor
von Neumann, härra Pitts ja mina ise aga olime matemaatikuteks.
Füsioloogid andsid küberneetika küsimustele ühise tõlgenduse oma
vaatekohalt, samuti nagu arvutite loojad esitasid omad meetodid ja
eesmärgid. Nõupidamise lõppedes oli saanud kõigile selgeks, et erisugustel
aladel töötajate vahel esineb põhimõtetes tugev üksmeel, et igasse
rühma kuuluvad inimesed võivad juba kasutada mõisteid, mida teised on
paremini arendanud, ja et tuleks teha teatavaid katseid ühise
sõnavara loomiseks.
vEEL k0Lm ALGEBRAL1st L61ku 
Veel ühe üldiselt mitteassotsiatiivsete, kuid assotsiatiivsetele ringidele küllalt lähedaste
ringide klassi moodustavad nn. alternatiivsed ringid, mille iga kahe elemendi a
ja b korral (aa)b=a(ab) ja (ba)a=b(aa),
s. t. assotsieeruvad selliste elementide järjestatud kolmikud, milles on kaks kõrvuti seisvat
võrdset elementi. Kui sümboliga [abc] tähistada elementide a,b ja c
nn. assotsiaatorit (ab)c-a(bc), siis võib alternatiivsuse tingimuse
esitada kujul [aab]=[baa]=0, samal ajal kui tavaline assotsiatiivsus on esitatav
kujul [abc]=0.
Antud hulga kõik alamhulgad ei moodusta ringi ühendi ja ühisosa võtmise operatsiooni suhtes,
sest kuigi need operatsioonid on omavahel seotud distributiivsuse seadusega (isegi kahe
distributiivsuse seadusega: (A
Struktuuride korral on liitmine ja korrutamine n.-ö. võrdõiguslikud, mis väljendub
neid siduvate tingimuste sümmeetrias: siin on mitte ainult liitmine, vaid ka korrutamine
kommutatiivne ja assotsiatiivne ning kehtib samuti liitmise distributiivsus korrutamise
suhtes. Peale selle kehtivad struktuurides ka mõlemad neelamisseadused.
topoLooGiLinE sEGAdus 
(Veidi lihtsustatud tõlge eesti keelde. Lause 6.4.6.)
Kui võrgu iga alamvõrk omab (alam-)alamvõrku, mis koondub elemendiks y, siis ka see võrk ise
koondub elemendiks y. Teisisõnu, kui võrk ei koondu elemendiks y, siis leidub
selle võrgu alamvõrk, mille ükski alamvõrk ei koondu elemendiks y.
Alates 15.02.02.  |
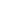 B)
B)  C =
(A
C =
(A